I once received a letter from a Twin Cam owner asking about the optimal shift points for achieving the best acceleration. His notion was that they were in the 4,500–5,000 rpm range. Given that his bike’s engine develops 108 hp at 5,800 rpm and 107 lb/ft of torque at 4,100 rpm, he didn’t display much understanding of the relationship between power, torque, and acceleration. He shouldn’t feel bad. Most of us don’t.
It’s a difficult relationship to master, because torque is physically tangible, whereas power is a more ephemeral calculated value. The mistake most folks make when engaging in this debate is considering horsepower and torque independently. Almost everyone argues as if they are separate, unrelated values. They aren’t.
In fact, there’s not a single machine in existence that measures horsepower. It’s a man-made number. When a vehicle’s performance is tested, its torque is measured using a dynamometer. The measure of an engine’s performance is torque. Horsepower is an additional number that’s attained by multiplying that torque by how often it’s repeated in a given span of time.
The common mistake
The truth is, horsepower is the by-product of torque and another value: rpm (divided by 5,252). It’s not unrelated, separate, or different, and anyone telling you that horsepower and torque should be considered equally and separately is significantly off-base. But to really understand power in general, regardless of how it’s labeled, one must start with the basic differences between force and work.
Force is a push or a pull exerted by one object on another. If you push on your bike, you are exerting a force on it. However, if it won’t roll you are not doing any work, because by definition work demands motion. Work equals force times distance. No matter how great the volume of sweat pouring off your brow as you push, if the scoot doesn’t move, even if it’s because you just left the damn thing in gear, no work is recognized (sweaty force x 0 = 0).
On the other hand, if a steady 100-pound force will move your motorcycle and you push it 50 feet, you have performed 5,000 ft/lbs of work (100 lbs x 50 ft). So far we haven’t said anything about time, but if you push it that 50 feet in 20 seconds, that’s a lot easier than doing so in five seconds, even though the work performed is 5,000 ft/lbs in each case. This difference leads us to the concept of power, which is the rate at which work is performed. Moving the motorcycle in 20 seconds requires a power level of 250 ft/lbs/sec (5,000/20), while doing so in five seconds requires 1,000 ft/lbs/sec (5,000/5).
Power also equals force times speed. In the first case, your speed of 2.5 ft/sec (50 ft/20 sec) multiplied by 100 lbs of force equals 250 ft/lbs/sec. At 10 ft/sec (50/5) we get 1,000 ft/lbs/sec. Whether calculated from work/time or force times speed, one horsepower is defined as 550 ft/lbs/sec.
An engine produces rotary motion (rather than the linear motion of the motorcycle) but the concepts are the same. Torque is simply the rotational equivalent of force. If you apply one pound of force to the end of a one-foot-long wrench, you are exerting one lb/ft of torque on the object you are trying to twist. To differentiate between the units for torque and work, we express torque in pound-feet (lb/ft) and work in foot-pounds (ft/lbs). As you might expect, the common unit of rotary speed is therefore revolutions per minute (rpm).
Multiply torque and rpm (the rotary equivalents of force and speed) and divide by a constant (to accommodate the switch from linear to rotational units and the conversion from ft/lb/sec to hp) and you have power (hp = torque x rpm/ 5,252). By reversing this basic power equation, we can see that while this guy’s engine develops its peak of 104 lb/ft of torque at 4,100 rpm, it only offers 94 lb/ft at its power peak (torque = hp x 5,252/rpm).
The physics of acceleration
What determines true acceleration for a vehicle isn’t really debatable; it’s work divided by mass. The confusion only comes in determining which work we’re actually talking about. We’ve already established that torque is the amount of rotational force being generated at the engine, but we aren’t concerned with the force at the engine. What we’re interested in is the work at the wheels. The work at the wheels is the w in w = ma. So, if we are solving for acceleration and we have a constant mass, that means… a = w/m.
The torque at the wheel is the torque at the engine combined with the torque “magnification” given by the transmission through gearing. So the transmission only sees what’s coming off the engine, while the wheels see the resulting force combination of the engine plus the transmission. That’s what horsepower represents. Horsepower is really the combination of the benefits of the engine’s raw abilities combined with rpm. And rpm is what allows us to use gearing effectively, which gives us more torque at the wheels. And that’s the trick to this whole mess. However, before we start short-shifting the engine to run it near the torque peak, we need to fully consider the effects of gearing.
Gearing magnifies torque
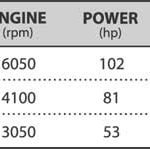
Gearing provides a way to trade off the two factors that create power: torque and rpm. To see how, we can calculate available power and torque from our friend’s Twin Cam at 55 mph in second, third, and fourth gears.
At this speed, the engine offers the most torque in third gear and the least torque in second gear. However, the task of accelerating the bike is performed at the rear wheel, where total torque equals engine torque times the transmission ratio times the final-drive ratio. So again we see, it’s the transmission that ultimately transmits the force to get work from the wheels, not the engine.
The figures confirm what most of us already know: Almost any vehicle invariably accelerates harder in the lowest available gear. That’s where the greatest horsepower is available. And because power is proportional to torque and speed, at any given speed you get the most torque at the rear wheel in the gear that lets the engine produce the greatest power. Therefore, for best acceleration, one should shift so as to maximize the engine’s power output.
This means never shifting lower than the engine’s power peak. The exact point can be determined if you know the engine’s power curve and the various transmission and final-drive ratios. But, even with nothing but a general seat-of-the-pants notion, it’s still obvious that the object is not to shift until there is more power available in the next higher gear. From first to second, for example, shifting at the 5,800 rpm power peak would drop the revs to about 3,400 rpm, where this particular engine can deliver no more than 58 hp. Even with the power falling past the power peak, there’s no percentage in going from a 104 hp point on the engine’s power curve to one 46 hp lower. In fact, even at its 6,500 rpm redline, this power plant is developing about 88 hp, which is more than the 70 hp available after the shift into second drops the engine to 3,825 rpm.
Shifting at redline is also the best you can do in second gear. But third and fourth gear are a bit closer together, so a redline shift will only drop the engine to about 4,800 rpm, where 93 hp is available. That suggests that a slightly earlier shift would better use the available power. In fact, by shifting at 6,400 rpm you can transfer the engine from the 93-hp-and-falling point on its power curve to 4,725 rpm, where the curve shows 93 hp and rising. From fourth to fifth, which are even more closely spaced, the ideal shift point is at 6,350 rpm. So yes, the answer to the question is torque, but torque at the wheels, not at the engine. And since we’re talking about torque at the wheels and not at the engine, the actual complete answer is horsepower, because horsepower encompasses not only the engine’s torque but the total power that gets put to the ground to work at accelerating the scooter!
With a low revving, high-torque engine like a Harley’s pushrod V-Twin, shift points can fall well below redline in every gear and acceleration won’t suffer too badly. (What the hey; it wasn’t that long ago that H-Ds had a mere four ratios or less to choose from in their trannys. It didn’t seem to hurt much.) That’s in sharp contrast to smaller, higher revving engines that make virtually all their power at high rpm and need precise use of a gearbox with lots of ratios to accelerate as quickly. But whether your particular Harley engine is a low-revving tractor or a 7,000 rpm screamer, you’ll get the best performance by shifting at the exact point where the grass is greener on the other side of the power curve.